The dregs of my notes on Polya’s Mathematics and Plausible Reasoning, Volume I:
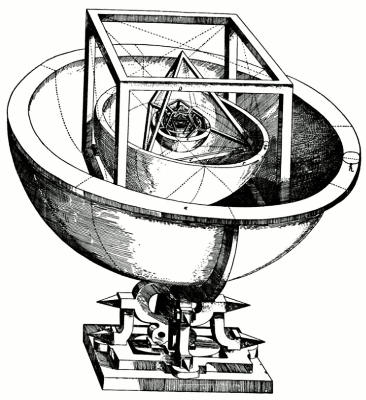
Polya discusses the 1595 work titled Mysterium Comographicum by the astronomer Johannes Kepler. Kepler believed that the orbits of the planets could be described as a series of standard solid geometic figures nested inside each other. It turns out that he was completely wrong, but his work and the way he TALKED about the problem was instrumental in leading others to the correct model later. He was in the middle (not the end) of breaking away from certain medieval ideas.
To modern eyes Kepler’s conjecture may look preposterous. We know many relations between observable facts and mathematical concepts, but these relations are of a quite different character. No useful relation is known to us which would have any appreciable analogy to Kepler’s conjecture. We find it most strange that Kepler could believe that there is anything deep hidden behind the number of the planets and could ask such a question : Why are there just six planets ?
We may be tempted to regard Kepler’s conjecture as a queer aberration. Yet we should consider the possibility that some theories which we are respectfully debating today may be considered as queer aberrations in a not far away future, if they are not completely forgotten. I think that Kepler’s conjecture is highly instructive. It shows with particular clarity a point that deserves to be borne in mind : the credence that we place in a conjecture is bound to depend on our whole background, on the whole scientific atmosphere of our time.
-p.198
This is good. This is an example of someone who looks at people in history and does not immediately assume they were behaving like a bunch of drooling idiots. They must have had good reasons for what they were doing. We just don’t understand their context. Perhaps our own context prevents us from seeing the silliness of our own ideas. What will people, especially scientists in our field a hundred years from now, think of what we are doing today?
—
If we examine a little the sequence of these numbers, we are almost driven to despair. We cannot hope to discover the least order.
-p.93
Geesh, that’s what I always feel when I look at a sequence of numbers that I’m supposed to find some secret pattern in. That stuff drives me nuts. I love patterns, but not in pure numbers. Give me context or give me death!
—
And since I must admit that I am not in a position to give it a rigorous demonstration, I will justify it by a sufficiently large number of examples.
-p.93
Again, an example of real intellectual honesty. Let’s have more of this and less B.S.
—
By the way, our example is quite rewarding (which is also typical). It leads to a curious relation between binomial coefficients.
-p.77
What? This interjection is in the middle of several thick pages explaining a number theory experiment (which I found utterly boring). It’s clear that he is finding delight in it! Different things float his boat than mine.
—
Do not ask unanswerable questions.
-p.70
—
Do you know what a “parallelepiped” is? I didn’t. You may know it by its name in the common tongue: a box.
—
Here is a hidden gem in the middle of a list of problems and examples for the reader to work through. The example discusses the probability of different eye colors appears in overlapping sets of girls.
You may try the experimental approach by looking into the eyes of several girls.
-p.120
(!!!)
Could be good advice to someone who reads too many books like this one.